Сложные проценты с ежемесячным внесением платежа

Выполняем просьбу пользователя frouzen, который просил написать Финансовый калькулятор. — рассчитывающий наращенную сумму при использовании сложных процентов и довложении средств ежемесячно равными платежами. Начисление процентов предполагается тоже ежемесячное (самый выгодный случай).

Чтобы не отвлекать пользователя от калькулятора, ниже идет сам калькулятор, а немного теории и формул надо смотреть под ним, кому не лень.

Калькулятор

Точность вычисления

Знаков после запятой: 2

Наращенная сумма

Сохранить share extension

Формула сложных процентов, начисляемых несколько раз в течении года
, где m в нашем случае равно 12, а n — срок вклада в годах

Это простейший случай при внесении вклада сразу, и без дальнейшего его пополнения.

Теперь займемся более сложным случаем — пополнением вклада одинаковыми платежами ежемесячно.
Заметим, что множитель степени mn не что иное, как число периодов начисления процентов.

Таким образом, для самого первого вклада за несколько лет наращенная сумма будет равна

Для вклада, который был внесен в конце первого месяца, число периодов начисления процентов на один меньше, и формула будет выглядеть так
,
для третьего вклада — так
,
…
и для последнего вклада, то есть внесенного за месяц до окончания срока — так
,

Интересующий нас результат равен сумме всех этих выражений. И эти выражения кое-что роднит — все они члены геометрической прогрессии, в которой первый член равен , а знаменатель прогрессии равен .

Про геометрическую прогрессию смотри Геометрическая прогрессия

Таким образом, искомая сумма по формуле суммы геометрической прогрессии равна

Вот и все на сегодня.

Обновление

По просьбе пользователя добавлена возможность отдельного указания размера первого взноса.

planetcalc.ru

Калькулятор сложных процентов: быстрый расчет онлайн

Главная / Калькулятор сложных процентов

Сложные проценты — когда проценты прибыли в конце каждого отчетного периода (в нашем случае дня) прибавляются к основной сумме и полученная величина в дальнейшем становится исходной для начисления новых процентов. Они часто используются при торговле криптовалютами трейдерами или сдачей в кредит в инструменте «Lending» на poloniex.com.

Формула расчета сложный процентов:

SUM = X * (1 + %)ⁿ

Где:

• SUM — конечная сумма;
• X — начальная сумма;
• % — процентная ставка, процентов /100;
• n — количество дней.

Как вы видите в калькуляторе идет расчет с ежедневной капитализацией, в poloniex.com же минимальный срок предоставление займа составляет 2 дня. Поэтому для расчета прибыли с выданного займа вам следуем проценты умножить на 2, а дни разделить 2.

Например:

• Процентная ставка: 0.18%
• Количество дней: 2
• Необходимо рассчитать прибыль за: 30 дней

В итоге в калькулятор вводим данные:

• Процентная ставка 0.36%
• Количество дней: 15

Сравнение сложного и простого процента

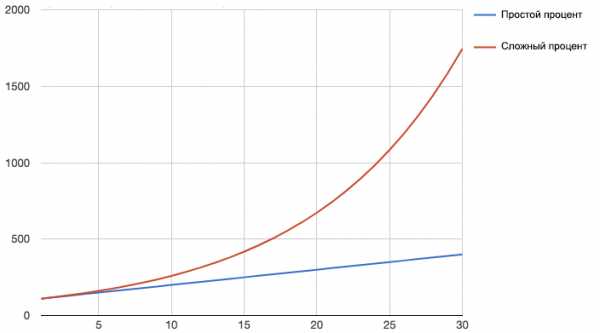
Сравнение сложных и простых процентов

Подробнее о сложных процентах на других сайтах:

icoinzzz.pro

Инвестиционный калькулятор сложный процент — Расчет онлайн

• Инвестиции
  • CointoniX Company
  • РосФинанс
  • Mizes
  • Nakopi Club
  • Dominant Finance
  • Супер Копилка
  • Wise Deposit
  • Right Робот
  • Платформа eToro
  • Бинариум
  • Amarkets
• Новичкам
  • Инвестиции в сети FAQ
  • С чего начать новичку
  • Куда инвестировать
  • Словарь Инвестора
  • Калькулятор Инвестора
  • Истории Успеха
  • Полезные Программы
  • Рефбек партнерам
  • Страховка инвестиций
  • Обмен валют онлайн
  • Курс криптовалют онлайн
  • Лучший инвестор месяца
• Обучение
• О блоге
  • Об авторе
  • Отзывы о блоге
  • Важная информация
• Контакты
  • Связь с автором
  • Реклама
• Личный кабинет

• Главная
• Что такое Форекс (Валютный рынок)?
• V.I.P. доступ к закрытой информации от Blogvestor.Biz по заработку 360-818% годовых!
• Робо-Тесты
• Обмен валют онлайн
• Управление подписками
• Поиск
• Важная информация
• Кабинет инвестора
• Услуги Листинга
• Курс криптовалют на сегодня в режиме реального времени!
• Новичкам
  • 1. Инвестиции в сети FAQ
  • 2. С чего начать новичку
  • 3. Куда инвестировать
  • 4. Рейтинг памм-счетов
  • 4. Словарь Инвестора
  • 5. Калькулятор Инвестора
  • 6. Истории Успеха
  • 7. Полезные Программы
  • 8. Рефбек партнерам
  • 9. Страховка инвестиций
• Отзывы о блоге
• Обучение
• Реклама
• Об авторе
• Контакты
• Статьи сайта

blogvestor.biz

Калькулятор онлайн — Сложные проценты. Депозитный калькулятор

Этот калькулятор вычисляет сумму срочного банковского вклада через указанный период, исходя из указанных процентов по вкладу.

Онлайн калькулятор для вычисления суммы вклада не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы вы могли проконтролировать ответ.

В банках для некоторых видов вкладов (так называемых срочных вкладов) принята система капитализации процентов. Т.е. проценты по вкладу в конце периода не выплачиваются вкладчику, а прибавляются к сумме вклада и на увеличенную сумму в конце следующего периода снова начисляются проценты. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода чисел

Числа можно вводить целые или дробные.

В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

В поле «Срок вклада» можно вводить только целые числа.

Введите сумму вклада, процент по вкладу и срок вклада

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т.д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или \( \frac{1}{100} \) часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100.

Например:

\( 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 \)

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

\( 0,58 = (0,58 \cdot 100)\% = 58\% \) \( 0,045 = (0,045 \cdot 100)\% = 4,5\% \)

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти \( \frac{p}{100} \) от a, надо a умножить на \( \frac{p}{100} \):

\( b = a \cdot \frac{p}{100} \)

Итак, чтобы найти р% от числа, надо это число умножить на дробь \( \frac{p}{100} \). Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью \( \frac{p}{100} , \; (p \neq 0) \), надо b разделить на \( \frac{p}{100} \):
\( a = b : \frac{p}{100} \)

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на \( \frac{p}{100} \). Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а \( (a \neq 0) \), надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

\( p = \frac{b}{a} \cdot 100\% \) Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют \( \frac{9 \cdot 100}{180} = 5\% \) раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

\( b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или \( \frac{pn}{100}S \), а всего придется заплатить \( S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S \)
Таким образом:
\( S_n = \left( 1+ \frac{pn}{100} \right) S \)

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
\( S_n = \left( 1- \frac{pn}{100} \right) S \)

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет \( \frac{p}{100}S \) р., и через год на счете окажется сумма
\( S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S \)
то есть начальная сумма увеличится в \( 1+ \frac{p}{100} \) раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
\( S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S \)

Аналогично \( S_3 = \left( 1+ \frac{p}{100} \right)^3 S \) и т.д. Другими словами, справедливо равенство
\( S_n = \left( 1+ \frac{p}{100} \right)^n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

www.mathsolution.ru

Калькулятор вкладов онлайн с капитализацией, с пополнением, рассчитайте процент доходности по депозиту в банке

Основная задача вкладчика – разместить свои сбережения на депозит, который принесет максимальный доход. Чтобы выяснить итоговую сумму вклада по окончании его срока и произвести расчет по доходу, порой бывает недостаточно знать размер годовой процентной ставки. Нужно воспользоваться калькулятором процентов по вкладам, ведь основные факторы, которые следует учитывать при расчете дохода, – это наличие капитализации и периодичность внесения дополнительных взносов в выбранный вами вклад. Кроме того, открывая вклад под высокую ставку, следует учитывать, что доходы по вкладам в РФ облагаются налогом в размере 35%, если процентная ставка по вкладу в рублях превышает ключевую ставку Банка России на 5 процентных пунктов, а по вкладу в иностранной валюте – на 9% годовых.

Калькулятор доходности вкладов на портале Банки.ру поможет произвести расчет суммы вклада с процентами. В депозитном калькуляторе указываете дату, когда вы планируете разместить сбережения в банке, например 15 апреля 2014 года, и срок привлечения вклада, который вы можете задать произвольно с точностью до одного дня. Депозитный калькулятор безошибочно определит день, когда вы сможете забрать свои сбережения вместе с начисленными процентами.

В калькуляторе депозитов можно сравнить сумму дохода в зависимости от того, будут проценты добавляться к сумме вклада либо выплачиваться на отдельный счет. Калькулятор вкладов с капитализацией покажет, как происходит расчет процентов и увеличивается сумма вашего вклада, ведь при выборе такого способа начисления проценты присоединяются к сумме вклада, тем самым увеличивая ее.

В калькуляторе вклада с пополнением необходимо будет указать периодичность, с которой вы планируете вносить дополнительные взносы, и сумму пополнений.

Калькулятор вкладов онлайн рассчитает для вас сумму дохода за вычетом налогов и покажет итоговую сумму вклада с начисленными процентами, в том числе с довложениями. Прежде чем открывать вклад в банке, с помощью калькулятора вкладов вы сможете вычислить доходность выбранного вами вклада с учетом всех его параметров.

Универсальный калькулятор вкладов на портале Банки.ру поможет нашим пользователям быстро произвести расчет вкладов и точно посчитать ожидаемый доход от своих сбережений.

www.banki.ru

Калькулятор сложного процента с капитализацией

Добрый день, дорогие читатели моего блога! Я уже не раз говорил, что депозит является одним из самых распространенных способов создания пассивного источника дохода. Поэтому часто меня спрашивают о таком понятии, как капитализация вклада и о формуле, которая позволяет сделать соответствующие расчеты.

И сегодня я решил рассказать об этой разновидности инвестиций, а также постараюсь дать некоторые рекомендации, как использовать калькулятор сложного процента с капитализацией.

Что такое капитализация

Очевидно, что деньги должны работать, чтобы приносить прибыль. Однако при этом важно правильно вложить свободные средства, чтобы исключить вероятность убытка.

Поскольку многие хотят делать выгодные инвестиции, но у них отсутствуют глубокие знания в области финансовой аналитики, то самым популярным решением становится открытие депозитного счета. В этом случае — в определенный период будет происходить начисление процентов на вложенную сумму.

В банковской сфере существует огромное количество неизвестных финансовых обозначений, которые вкладчики вполне могут встретить в своем договоре.

Одним из таких терминов является «капитализация». Под этим словом понимают, что каждые последующие начисления прибавляются к основной сумме депозита.

Например, вы вложили 1000 долларов, через год на эту сумму было начислено 20% годовых или 200 долларов. Таким образом, общая сумма на счету составит 1200 долларов. В следующем году 20% будет начисляться уже не на 1000 долларов, а на 1200 долларов. Доход составит 240 долларов. Еще через 12 месяцев 20% будут начисляться уже на сумму 1420 долларов.

Благодаря такому варианту сотрудничества с банком доход будет приносить не только первоначально вложенные средства, но и деньги, начисленные в соответствии со ставкой.

Часто можно услышать, что такие инвестиции называют вкладами со сложными процентами. Они являются достаточно выгодными, поскольку конечная ставка по такому вкладу является гораздо более высокой, чем первоначальная.

Существуют депозиты, которые позволяет осуществлять прибавку начислений к основной сумме каждый месяц, раз в квартал или раз в год. Справедливости ради замечу, что периодичность капитализации и начисления процентов — это два разных понятия.

Например, учреждение по условиям договора может выполнять начисление процентов на вложенную сумму каждый день, но прибавка их будет происходить раз в 30 дней. Возможны другие условия сотрудничества с банком. Их нужно уточнять со специалистом при оформлении договора.

Как считать доход с помощью онлайн-калькулятора

Для этого существует немало онлайн калькуляторов, которые позволяют сделать точные расчеты. Чтобы посчитать доход по вкладу с эффективной ставкой, необходимо в онлайн калькуляторе указать размер вложения, валюту, в которой он будет сделан.

Также потребуется выбрать дату вклада, ставку, срок, план начисления процентов, порядок налогообложения.

Если депозит оформляется с эффективной ставкой, то нужно поставить галочку напротив этого пункта. Также для корректного расчета необходимо выбрать, как по договору учитываются выходные и праздничные дни.

Кроме того калькулятор позволяет уточнить график пополнений, частичного снятия, а также пролонгации. После того как все данные будут введены, нужно нажать на кнопку «расчет» и ознакомиться с полученными цифрами. В зависимости от типа онлайн калькулятора вводные данные могут меняться.

Достоинства и недостатки вкладов с капитализацией

Если вы хотите ежемесячно получать добавку к своему основному доходу, то простой депозит окажется более выгодным. Полученный доход будет поступать на расчетный счет. При оформлении вклада с эффективной ставкой же отсутствует возможность частично снимать средства в период размещения.

Этот вариант не всегда подходят людям, которые хотят перестраховаться и иметь возможность забрать свои денежные средства при любой экономической нестабильности в стране или при возникновении личных трудностей.

Финансовые учреждения, которые предлагают вклады с эффективной ставкой, зачастую уменьшают на них размер ставки. Таким образом, итоговая разница между простым депозитом и вкладом со сложным процентом фактически отсутствует.

Если же у вас есть свободные денежные средства и желание обеспечить постоянно растущие суммы выплат, то депозит с капитализацией станет эффективным и удобным инструментом для получения прибыли.

Что следует учесть при выборе типа вклада

В первую очередь, нужно оценить свои возможности, а также потребности в денежных средствах в ближайшем будущем.

Если вы считаете, что долгое время средства с депозитного счета не понадобятся, то в качестве стратегии накопления можно выбрать капитализацию. После этого следует обратить внимание на предложения банков.

Обращайтесь в то учреждение, где эффективная ставка будет наибольшей.

Обязательно проанализируйте все составляющие конкретной депозитной программы и сравните условия размещения средств. Особое внимание уделите надежности банка, поскольку от этого зависит сохранность финансовых средств.

Главное, помните, что не стоит вкладывать все свои деньги в один единственный банк. Чтобы минимизировать риски, стоит использовать разные финансовые инструменты.

Если вам понравилась моя статья, то не забывайте оставлять комментарии, чтобы я знал, насколько этот материал был полезен.

Для тех, кто только присоединился к блогу, рекомендую подписаться на обновления, чтобы первым быть в курсе выхода новых статей.

Подписывайтесь также на Телеграм канал — t.me/investbro_ru. До новых встреч!

investbro.ru

Калькулятор сложных процентов — Кто в Деле | Как открыть свой бизнес с нуля

Калькулятор сложных процентов станет помощником при осуществлении расчета прибыли с депозита с реинвестицией процентов. Это капитализация, которая означает — каждый день, либо месяц к вкладу будет добавлена сумма процентов, впоследствии используемая как база для последующего начисления.

Правила работы с инструментом

Сервис производит вычисления, согласно стандартным формулам для сложных процентов для депозитных вкладов:

SUM = X * (1+%)n,

где SUM – это сумма итога к получению, Х – величина вклада (первоначальная), % – процентная ставка (годовые), n – количество месяцев, либо лет.

В свою очередь, ставка % считается:

% = p * dy,

где р – процентная ставка по конкретному вкладу, d – сколько дней в периоде (по его итогам происходит реинвестиция), y – количество календарных дней в году.

Тогда формула сложных процентов по вкладу принимает вид:

SUM = X * (1 + p * dy)n

Производя вычисления для большого количества лет легко допустить ошибку и прийти к неверному результату. Поэтому нужно использовать калькулятор сложных процентов, который произведет все вычисления автоматически.

Алгоритм использования инструмента

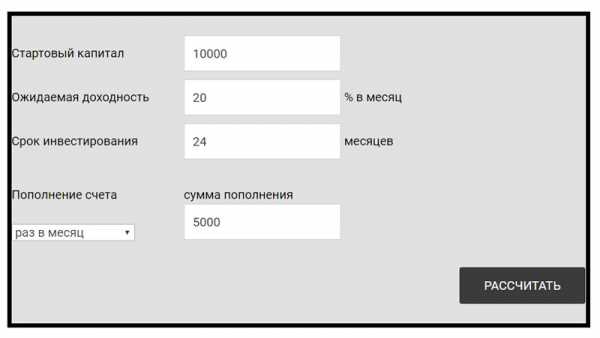
Чтобы определить доход по вкладу с капитализацией, нужно ввести несколько значений в ячейки:

• начальный депозит – укажите сумму вклада;
• количество периодов – в годах или месяцах;
• доходность за 1 период – ставка % в год или в месяц;
• довложения за период – используется при оформлении депозита с довложениями, если вклад без дополнительных взносов – оставьте это поле пустым.

Нажмите кнопку «Рассчитать» и система выдаст вам расчеты доходности депозита в таблице, согласно указанному периоду.

ktovdele.ru